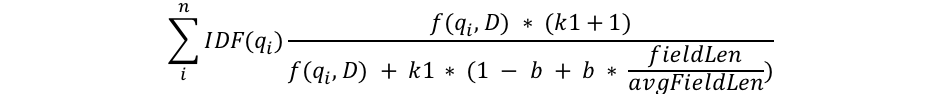はじめまして、DevOps チームの中島です。
レアジョブ社の技術部門は、4 月 1 日 から新たにレアジョブテクノロジーズ社としてスタートしました。
新しい組織ではフルリモート可となっており、私も都内から引っ越して田舎暮らしを満喫しています。
さて今回は、 Elasticsearch (Lucene) のコードを読んでいく中で見つけた実装の工夫について紹介したいと思います。 レアジョブのサービスでも Elasticsearch を全文検索に利用している箇所があります。 OSS である Elasticsearch のコードを読み込むことで、高速化や検索精度の向上、その他プロダクトの品質向上に繋げたいと考えこのような取り組みをしています。
基礎知識
検索対象のデータ (インデックス) はストレージに保存されており、 Lucene はその内容をメモリに読み込みながら該当データの検索を行います。 データを効率よくエンコードしてストレージに保存することで、 単純に読み書きの量が減る、OS のバッファキャッシュにヒットする確率が上がる、等により検索速度の向上に繋がります。 以下では Lucene で実装されているエンコードの工夫について紹介します。
1. 可変長数値のエンコード
同じ数値型を等しいバイト数ではなく可変長で表現することで、小さい値のバイト数を節約するエンコード方式です。 最上位ビットを次のバイトが存在するフラグとして扱うことで実現しています。 代表的なところでは、Thrift や Protocol Buffers でも採用されています。 例えば、以下のように各値をバイト列で表現します。
値 バイト列 2^7 01000000 2^14 01000000 10000000 2^21 01000000 10000000 10000000 ...
値を読み込むコードは以下です。
読み込んだ各バイトの最上位ビットが立っている場合 ( !b>=0 ) 、次のバイトを読み込んでいます。
// org.apache.lucene.store.DataInput public int readVInt() throws IOException { byte b = readByte(); if (b >= 0) return b; int i = b & 0x7F; b = readByte(); i |= (b & 0x7F) << 7; if (b >= 0) return i; b = readByte(); i |= (b & 0x7F) << 14; if (b >= 0) return i; ...
2. ドキュメント ID と単語の出現頻度のエンコード
全文検索エンジンは、検索対象の単語が出現するドキュメントを提示するだけでなく、
関連するドキュメントがより上位にくるように並び替える機能を提供する必要があります。
この並び替える機能は、検索クエリに対する各ドキュメントの関連度 (スコア) をドキュメントごとに計算し (スコアリング) 、
スコアの高い順に並び替えることで実現されています。
古くから文書検索においては、ドキュメント*1内の単語の出現頻度をスコアリングに使用しています。 検索クエリ内の単語が多く出現すれば、より関連度が高いドキュメントだろうという想定です。 この単語の出現頻度を記録するインデックスファイルの内容は、概念的に以下のようになっています。
フィールド f1
単語 t1
ドキュメント ID1, t1 の出現頻度
ドキュメント ID2, t1 の出現頻度
ドキュメント ID3, t1 の出現頻度
(=フィールド f1 内に 単語 t1 が出現するドキュメント ID、その出現回数)
...
このうち、ドキュメント ID と出現頻度が繰り返される部分において、以下のような実装になっています。
- ドキュメント ID 部分は前レコードのドキュメント ID との差分を格納する
- 出現頻度が 1 の場合、ドキュメント ID 部分は ドキュメント ID を 1bit 左シフトして最下位ビットを立てる
(出現頻度が 2 以上 の場合、ドキュメント ID を 1bit 左シフトした値を格納し、普通に出現頻度のバイト列を続ける)
つまりは、以下のような工夫がなされています。
- 連続する数値を格納する際に、差分を格納することでビット数を削減する
- 同じ単語が一度しか出現しない確率が高いという特性を利用して最適化が行われている
値を読み込む部分のコードは以下です。
docID 変数には前レコードの docID が入っています。
ドキュメント ID として読みこんだ値 (code) を 1bit 右シフトして docID に加算し、該当レコードの ドキュメント ID としています。
その後、最下位ビットの判定から出現頻度 (freq) を読み込んでいます。
// org.apache.lucene.index.FreqProxDocsEnum public int nextDoc() throws IOException { ... int code = reader.readVInt(); if (!readTermFreq) { ... } else { docID += code >>> 1; if ((code & 1) != 0) { freq = 1; } else { freq = reader.readVInt(); } } ... }
3. 指数表現によるエンコード
Elasticsearch における text フィールドの検索は、標準で BM25 と呼ばれるスコアリングアルゴリズムが採用されています。
引用元: Practical BM25 - Part 2: The BM25 Algorithm and its Variables | Elastic Blog
細かい計算方法は他所に譲りますが、スコアリングに必要な情報がインデックスファイルに格納されていて、それを読み込みながら計算が行われます。
ここで紹介するのは上記の計算式に出てくるドキュメント長 (fieldLen)*2 です。
ドキュメント長はドキュメント内の単語の数を表していて、最大 232 - 1 = 4 バイト分の値の範囲を取るのですが、
浮動小数点数のような指数表現を用い、精度を落とすことで 1 バイトに変換された値がインデックスに格納されています。
1 バイト (8bit) のうち、先頭 5bit が指数部、末尾 3 bit が端数を表しています。
正確にはインデックスに格納される値 = (24 + α) のうち α の部分が上記で表現されます。
24 は 以下に示す longToInt4 メソッドを用いて Integer.MAX_VALUE を表現した値である 231 を、 1 バイトで表現できる最大長である 255 から引いた値です。可能な限り小さい値は正確に表現したいことが分かります。
α の部分をエンコードするコードは以下です。
// org.apache.lucene.util.SmallFloat public static int longToInt4(long i) { ... int numBits = 64 - Long.numberOfLeadingZeros(i); if (numBits < 4) { // subnormal value return Math.toIntExact(i); } else { // normal value int shift = numBits - 4; // only keep the 5 most significant bits int encoded = Math.toIntExact(i >>> shift); // clear the most significant bit, which is implicit encoded &= 0x07; // encode the shift, adding 1 because 0 is reserved for subnormal values encoded |= (shift + 1) << 3; return encoded; } }
終わりに
振り返ってみると全部エンコードの話になってしまいました。
コードリーディングをすると様々な効率化の工夫を発見出来て楽しいですね。
最後までご覧頂きありがとうございました。
We're hiring!